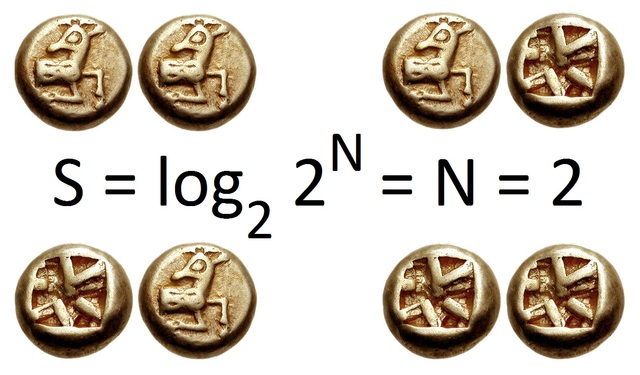抛硬币与计算机中的“数据”
date
Mar 26, 2020
note
slug
coins-and-data
type
Post
status
Published
tags
技术
入门
summary
最近与几个朋友聊到了“信息的本质”相关的话题,惊讶地发现,即使是计算机相关专业在读,面对“数据究竟是怎么一回事”这个问题,许多人依然云里雾里(包括我)。
解决了这个最根本的问题,方可从计算机领域的各种复杂之中解脱出来。所以我也尝试以文章的形式梳理一下。
最近与几个朋友聊到“信息的本质”相关的话题,惊讶地发现,即使是计算机相关专业在读,面对“数据究竟是怎么一回事”这个问题,许多人依然云里雾里(包括我)。
解决了这个最根本的问题,方可从计算机领域的各种复杂之中得以解脱。所以我也尝试以文章的形式梳理一下。
“数据” 与 “信息”
说到“数据”,自然和“信息”这个概念是分不开的。什么是信息呢?这个概念没有一个统一定义,但有一点可以确认的是:信息可以减少不确定性。对一件事情不确定,引入信息,把不确定变成确定,这是最基本的“通信“过程。
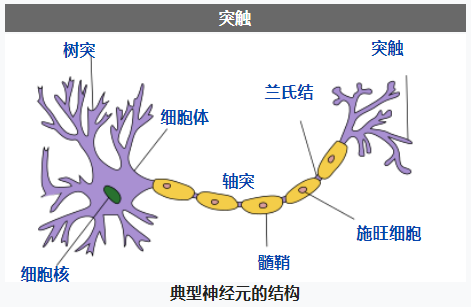
“通信”过程时时刻刻都在发生,你的肉眼看到的每一个画面,耳朵听到的每一点声音,神经传来的每一丝冲动,或多或少都在传递着信息,为你的大脑减少对外界的不确定性,辅助你的每一个决策。
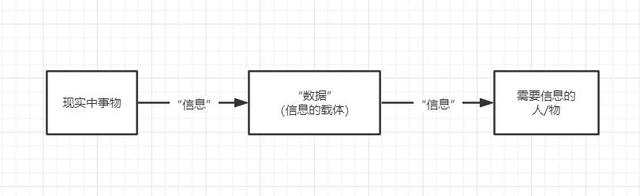
这时候,“数据”像是一种客观角度下的“信息”存在,它从某个具体的角度描述了某个事物的特征。当我们需要确定某事物在某个角度的特点,这个角度对应的“数据”便可以给我们传递应有的信息。比如说,我想知道你的期末考试成绩如何,成绩单上对应这门课的数字,可以给我带来这方面的“信息”;我们看到一段文字、一张照片,了解到一件事情的来龙去脉,文字和照片传递了“信息”,这段文字、这张照片本身就是“数据”。
从这个角度上来看,“数据”实际上是“信息”的载体,我们从某个角度,解决对客观事物的不确定性,形成“数据”;然后我们再通过“数据”解决我们自身对客观事物的不确定性。也就是说,“数据”给我们传递了“信息”。以本文为例,我用文字记下了这篇文章,你在读这篇文章的时候,了解了我所讨论的“数据”与“信息”是怎么一回事。
香农与信息的度量
上一小节的讨论只是一个粗略的印象,更上一层的讨论与发展应用,只有把根基确定下来才好继续进行。
1948年,美国数学家 克劳德·香农 发表了论文《通信的数学原理》,奠定了信息论的基础,确定了更上一层讨论发展赖以生存的根基。目前计算机领域有关信息处理的一切,都是在香农信息论的框架之下进一步发展出来的。
香农把热力学的熵引入信息论,给出了信息熵(一般也叫“信息量”)的定义,它是一串不那么直观的数学公式,这个公式表示的是整个随机事件 𝑋X 信息量的数学期望:
其中:
为一个随机事件,可能有 , , ..., 这 种情况 为 发生的概率, 为 发生对应的信息量 为对数的底
当 ,熵的单位是
bit (比特),当 ,熵的单位是 nat (奈特),当 ,熵的单位是 Hart。在香农信息论下,我们有了一个准确度量信息的方法,为后面更多的数据处理过程打下了坚实的基础。
抛硬币问题
上面我们谈到了
bit,有的同学可能有所察觉,这个 bit 单位和计算机的 bit 是不是同一个东西?答案自然是的。实际上,计算机领域的信息传递,归根结底符合一个类似“确定抛硬币的结果”的数学模型。
我们知道,抛出一枚硬币,落到地上,只有正面反面两种情况(不要问我为什么不能立起来),它们发生的概率各为 。也就是说,我抛出一枚硬币,落地后它有两种可能:
- 可能是正面
- 可能是反面
然后我去看地上的硬币,这时两种“可能”变成了一个“确定”的结果,“就是正面” 或者 “就是反面”。
在香农的理论下,我们可以推导出这个确定结果的过程对应传递的信息量。
假设条件:
:抛一枚硬币,正反面两种情况 ,:我们用 bit 作为单位
那么,信息量 即为:
到这里我们知道了,从抛一次硬币的两种可能(正面 / 反面)之中确定一个结果的信息量,恰好就是 1 bit。
计算机的抛硬币模型
计算机存储与处理数据最基本的单位,依赖于某种具有两种状态的现实事物。比如说开关的通与断、灯泡的亮与灭、晶体管的导通和截止、电位的高电平与低电平等等。计算机领域所做的,正是为它们的两个状态分别赋予特定的意义。
在数学的角度,我们把二进制数字两个符号("0" 和 "1")的意义赋予到机器层面的这两个状态上,这时候基于 0 与 1 的二进制算术的规律也一起赋予到了这上面。当我们在机器层面按照二进制算术中的加法、减法、移位等运算把对应的状态转移机制实现,就把二进制算术的计算过程变成了可以运行的现实。

在信息的角度,我们把前面提到的“抛硬币模型”赋予到计算机上面,把抛出一枚硬币得到的“正面”、“反面”的结果,对应到机器里面“开关”的“通”、“断”两种状态。由于计算机内部有成千上万个这样的“开关”,也就是说,它可以为我们确定抛成千上万次硬币、落地后的最终结果。
为了方便描述问题,原本一枚硬币抛成千上万次的过程,等价为“一次抛出成千上万枚硬币”之后,确定每一枚硬币的正反面状况。这时每一枚硬币只有一次被抛出的机会,那一枚硬币代表的信息量(熵)就是 1 bit。
当我们把机器层面的“开关的两种状态”、数学角度的“二进制算术”、信息论角度的“抛硬币模型”联系在一起以后,我们眼中的计算机就拥有了基本的数据处理能力。
想像下,你眼前的手机或电脑,内部每时每刻都有无数“硬币”在其中不断翻转,是不是很壮观!
为硬币赋予现实意义
到这里我们抽象出了一个“硬币”的模型,就不用去关心计算机究竟是怎么实现的,管它是用灯泡、还是开关、亦或是晶体管。
我只需要关心这样的事实:一枚硬币,可以给我确定 1 bit 的信息,可以从正面或反面两种可能中确定一个结果;两枚硬币,可以从 种可能中确定一个结果,信息量 2 bit;三枚硬币,就是 种可能中确定一个结果,信息量 3 bit ...
是的,计算机给我们提供了大量的硬币给我们使用,我们要做的,便是把这样的硬币和我们想让计算机做的事情联系在一起。
我们以三枚硬币(3 bit)为例,它所能够表示的 8 种可能状态列出来如下表:
硬币1 | 硬币2 | 硬币3 |
反 | 反 | 反 |
反 | 反 | 正 |
反 | 正 | 反 |
反 | 正 | 正 |
正 | 反 | 反 |
正 | 反 | 正 |
正 | 正 | 反 |
正 | 正 | 正 |
我们有了
反反反、反反正、反正反、反正正... 这 8 种可能状态,各自赋予一个具体意义,然后我们就能用 3 枚硬币去表达我们需要表达的东西。我们以 8 进制数为例,看我们是怎么把 8 进制数的意义体系赋予到硬币上。
硬币1 | 硬币2 | 硬币3 | 赋予 8 进制数的意义 |
反 | 反 | 反 | 0 |
反 | 反 | 正 | 1 |
反 | 正 | 反 | 2 |
反 | 正 | 正 | 3 |
正 | 反 | 反 | 4 |
正 | 反 | 正 | 5 |
正 | 正 | 反 | 6 |
正 | 正 | 正 | 7 |
此时我们有了:
反反反 <--> 0
假设我们需要在八进制意义体系下表达十进制的
10,也就是八进制下的符号 12。1 和 2 两个符号的“硬币表示法”分别是:反反正、反正反。也就是说,我们想表达十进制意义体系下的数字
10,以上面的八进制意义体系,再对应到计算机里面已实现的“硬币体系”的表达,需要六枚硬币摆成 反反正反正反 的状态,带来 6 bit 的信息量。有没有一种“结绳记事”的味道?这里我把它叫做“摆硬币记事”。
英文字符的表示
上面我们为“硬币体系”赋予了八进制数字角度的意义,让计算机处理数学运算成为了可能。但机器总归是为人服务的,不可能总在处理上古时期的打孔纸带,为了处理更多类型的数据,需要有更多角度的意义体系赋予到硬币上。
接下来简单介绍下我们怎么为“硬币体系”赋予英文字符角度的意义。
假设我们只需要表示英文字母和数字。英文有26个字母,区分大小写,则有 52 个字符,加上 0-9 10个阿拉伯数字,有 62 个字符,也就是说,我们需要 62 种状态去赋予各个符号的意义。至少需要 6 枚硬币所能确定的 种状态才可以表示。
这里产生了一个问题,我们自己发明的意义是很难考虑的很周到,在意义体系成型后,你需要向使用者讲述这里的约定,得付出大量的沟通成本。在这个角度,计算机世界的前辈们其实在很早就针对这个问题达成了一个共识,设计了一个通用的“意义体系”,那就是 ASCII,ASCII 是啥?

ASCII 全称 American Standard Code for Information Interchange (美国信息交换标准代码),它设计了现代英语字符与电脑的”硬币体系“的对应关系,它从1963年第一版发布到1986年最后一次更新,一共定义了 128 个字符。
为了方便表示,我们给硬币正反两面各自赋予一个符号,用数字 1 和 0,也就是数学里的二进制数。然后字母、数字和一部分字符和二进制位(硬币)的对应关系如下:
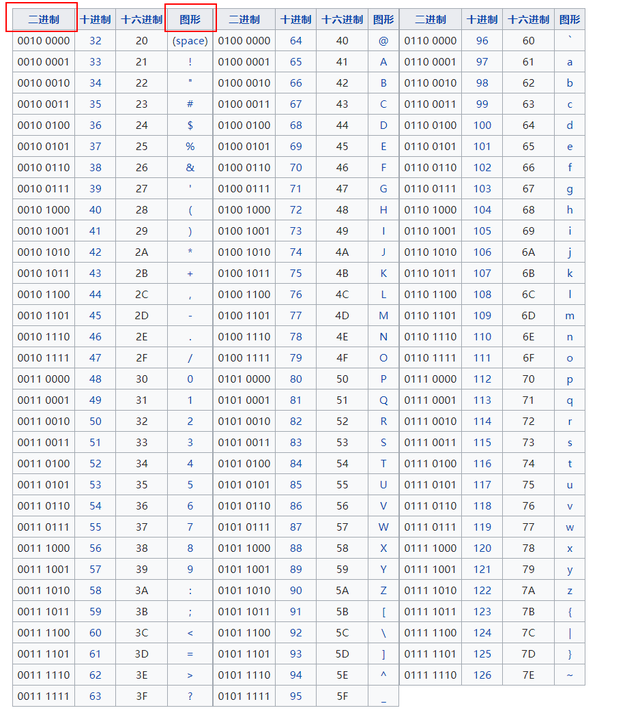
在计算机中,我们用 8 个二进制位(硬币)来表示一个 ASCII 字符。实际上它只用到后 7 位(),第一位都是 0,参考下表:
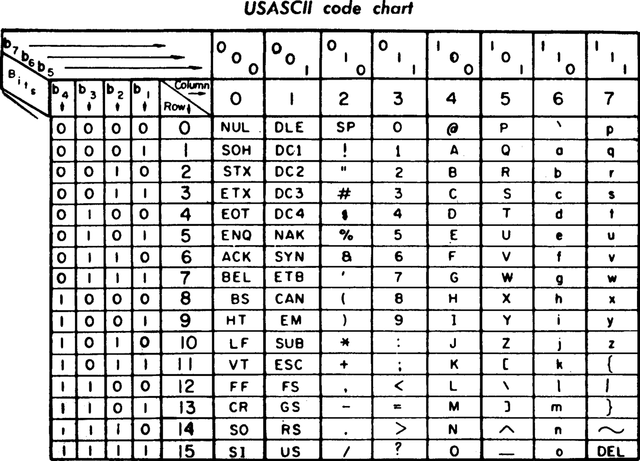
在机器操作的效率等方面的考虑下,ASCII 的有的位还有一些特殊的意义,比如说,表中 这一位为
0 时,对应大写字母,为 1 时则是小写字母,利用这个规律,大小写转换就变得十分简单。到这里我们可以明确计算机描述现实数据的基本规律:
- 计算机在硬件上实现稳定的“二进制-硬币体系”
- 使用者为体系中硬币组成的各个状态赋予意义
- 根据意义,将现实数据转换为硬币角度的表示
现实中我们有更复杂的数字、文字、图片、视频和声音,数据多种多样,我们怎么用硬币和硬币之间的组合表示它们呢?限于篇幅,我们下篇文章再讨论这个话题吧~
数据量单位
前面提到,我们用许许多多的“硬币”去表示数据。保存数据(一系列“硬币”的正反状态)需要消耗仓库的空间、拷贝/传输数据(复制硬币摆放的状态)也需要成本。因此,某段数据本身的大小、空间占用、传输流量也是我们常关心的话题。
是的,这里我想说的就是
b, B, KB, MB, GB 等数据量单位的具体含义。明确了 “硬币” 的基本模型,理解这些单位自然也是水到渠成。首先是最基本的单位,
bit,简写 b,中文“比特”,就是前面我们提到的,在香农的理论体系下,确定一枚硬币正反面的信息量。然后是
B, Byte ,中文翻译“字节”,电脑的 CPU、内存、网络 等等均以 Byte 为最小的单位交换数据,所以说,我们日常接触到的最基本数据量单位都是 Byte。一个 Byte 包含了 8 个 bit。用 “硬币体系” 的话就是说,电脑每一次抛出的硬币个数都是 8 的倍数。KB ,KiloByte,千字节,顾名思义,1KB = 1000B。MB ,MegaByte,兆字节,1MB = 1000 KB = 1000,000B。GB ,GigaByte,吉字节,1GB = 1000 MB = 1000,000KB = 1000,000,000B。TB ,TeraByte,太字节,以此类推...二进制与十进制单位
到这里,你可能会有一个疑惑:我们常说 1KB = 1024B,为什么这里是 1000 呢?这里涉及到了千位进位时,采取十进制国际单位制还是二进制单位、以及两者的混淆问题。
1000 这个倍数并不容易简单地通过移位操作(增加或减少“硬币”)的方式来实现,在机器角度实现复杂度要高许多;而 210=1024210=1024,约等于 1000,恰好是移动 10 个二进制位的事情,所以人们也常用 1024 来做换算。这种方法暂时没找到合适的定义,这里我把它称为“千位二进制进位法”。
严格意义来说,采用这种 “千位二进制进位法” 产生的单位,简称不应该是
KB,而是 KiB,全称Kibibyte,是 Kilo Binary Byte 的缩写,这是混淆的根源。到这里我们已经基本把问题解释清楚了,更具体的表示,参考维基百科的 Kibibyte 词条下的数据量单位换算表格,如下图:
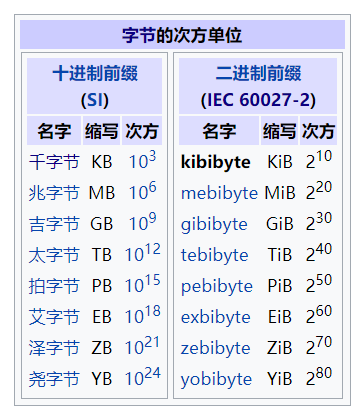
在计算机网络、硬盘、U盘、光盘等存储器领域,常用十进制的国际单位制来转换。但占领了几乎全球绝大部分个人电脑的微软 Windows 操作系统中大量使用 “千位二进制进位法” 做单位转换,以及电脑的 CPU 缓存和内存条制造时为考虑到方便寻址,也采用二进制法凑整,造成了更多的混淆。(这也是为什么显示的硬盘容量要比标称的要小许多)
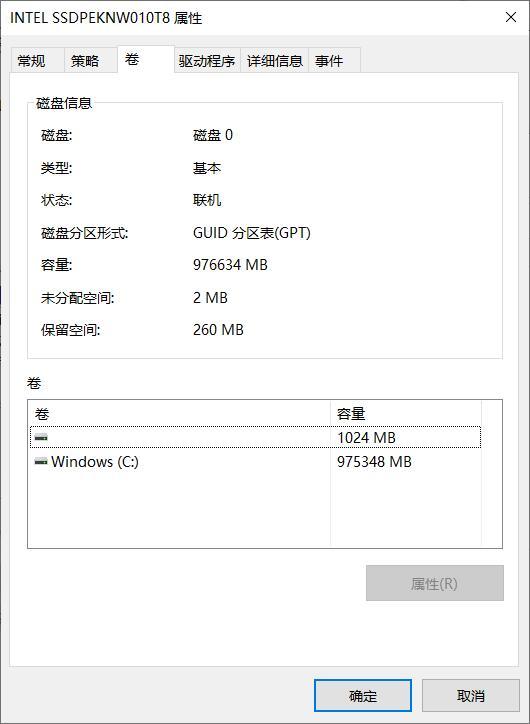
由于混淆已经普遍化,如今我们常说的
KB 也常常指的是 Kibibyte 了。